Jenis Bangun Ruang Sisi Lengkung – Apa itu bangun ruang sisi lengkung? Apa saja jenis bangun ruang sisi lengkung? Sebutkan unsur-unsur bangun ruang sisi lengkung! Sebutkan rumus bangun ruang sisi lengkung beserta contoh soal! Apa saja contoh benda bangun ruang sisi lengkung?
Agar lebih memahaminya, kali ini kita akan membahas tentang pengertian bangun ruang sisi lengkung, jenis, unsur, rumus, contoh soal bangun ruang sisi lengkung dan pembahasannya secara lengkap.
Pengertian Bangun Ruang Sisi Lengkung
Bangun ruang sisi lengkung adalah kelompok bangun ruang yang memiliki bagian-bagian yang berbentuk lengkungan. Biasanya bangun ruang ini memiliki selimut ataupun permukaan bidang.
Bangun ruang sisi lengkung merupakan bangun ruang yang punya bagian berupa lengkungan baik selimut atau permukaan bidangnya.
Jenis-Jenis Bangun Ruang Sisi Lengkung
Yang termasuk macam-macam bangun ruang sisi lengkung diantaranya tabung, kerucut dan bola.
Tabung
Tabung adalah sebuah bangun ruang tiga dimensi yang memiliki tutup dan alas yang berbentuk sebuah lingkaran dengan ukuran yang sama dengan di selimuti oleh persegi panjang. Tabung juga disebut dengan silinder.
Contoh benda berbentuk tabung yang bisa ditemui di kehidupan sehari-hari diantaranya gelas, kaleng susu, drum, botol, seruling dan lain sebagainya. Berikut ini gambar tabung:
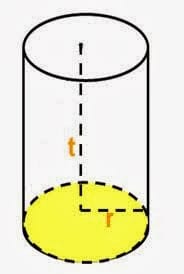
Sifat-Sifat Bangun Tabung
Sifat atau ciri-ciri tabung, diantaranya yaitu:
- Memiliki 2 (dua) buah rusuk lengkung.
- Memiliki alas dan tutup berbentuk lingkaran yang masing-masing sama besar.
- Memiliki 3 (tiga) buah sisi diantaranya dua buah sisi berbentuk lingkaran dan satu sisi selimut berbentuk persegi panjang.
- Tidak memiliki titik sudut
Jenis-Jenis Tabung
Terdapat 2 (dua) jenis tabung, diantaranya:
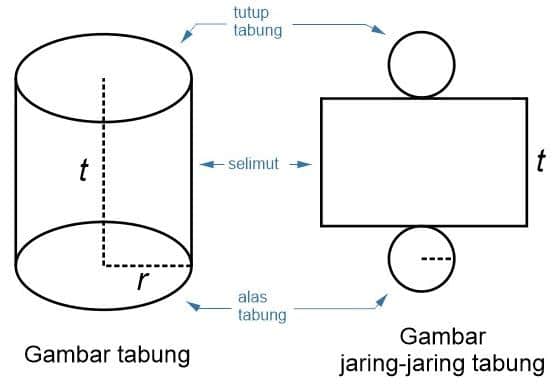
Tabung Tertutup
Tabung Tertutup adalah sebuah tabung yang seluruh bidang dan sisi-sisinya tertutup.
Tabung Terbuka
Tabung terbuka atau tabung tanpa tutup adalah sebuah tabung yang salah satu sisi alasnya atau sisi atapnya terbuka bahkan keduanya antara sisi alas dan sisi atapnya juga terbuka. Karena tidak memiliki tutup, maka luas sisi tutup tabung yang berupa lingkaran tersebut tidak dihitung.
Rumus luas tutup tabung : 2πr
Rumus luas alas tabung : 2πr
Rumus luas selimut tabung : 2πr²t
Karena tanpa tutup, maka rumus luas permukaan tabung tanpa tutup bisa disimpulkan:
Luas tabung tanpa tutup = π x r2 + 2 x π x r x t = π x r (r + 2t)
Unsur-Unsur Tabung
Berikut ini unsur atau bagian tabung, diantaranya yaitu:
Tinggi Tabung
Tinggi tabung adalah jarak antara bidang alas dan juga bidang tutup pada tabung yang biasa dinotasikan dengan menggunakan huruf t.
Jari-Jari Tabung
Jari-jari (r) adalah jarak dari titik pusat ke titik lain diluar bola.
Diameter Tabung
Diameter (d) adalah jarak antara dua titik terluar bola yang melewati titik pusat bola. Panjang diameter sama dengan 2x panjang jari-jari.
Sisi Tabung
Sisi adalah kumpulan titik yang berjarak sama dengan titik pusat.
Rumus Tabung
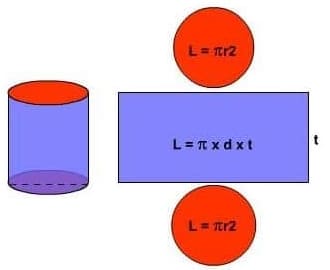
Secara singkat rumus tabung yaitu:
Rumus Keliling Alas Tabung = 2πr
Rumus Volume Tabung (V) = πr²t
Rumus Luas Tabung (L) = 2πr²
Rumus Luas Alas = Luas Lingkaran = πr²
Rumus Luas Tutup = Luas Alas = πr²
Rumus Luas Selimut = Keliling Alas × Tinggi = 2πr × t = 2πrt
Rumus Luas Permukaan Tabung = Luas Alas + Luas Tutup + Luas Selimut
Rumus Luas Permukaan Tabung = 2πr² + 2πrt
Rumus Luas Permukaan Tabung = πr² + πr² + 2πrt
Rumus Luas Permukaan Tabung = 2πr(r + t)
Rumus Volume Tabung = Luas Alas × Tinggi
Rumus Volume Tabung = πr²t
Rumus kerucut + tabung:
Rumus volume = (π.r².t )+(1/3.π.r².t)
Rumus luas = (π.r²)+(2.π.r.t)+(π.r.s)
Rumus tabung + 1/2 bola:
Rumus menghitung Volume = π.r².t+2/3. π.r³
Rumus menghitung Luas = (π.r²)+(2.π.r.t)+(½.4.n.r²) = (3.π.r²)+(2. π .r.t)
Rumus tabung+bola:
Rumus untuk menghitung Volume= (π.r².t)+(4/3. π.r³)
Rumus untuk menghitung Luas= (2. π.r²)+(4. π.r²) = π.r²
Keterangan:
V = Volume tabung(cm3)
π = 22/7 atau 3,14
r = Jari-jari /setengah diameter (cm)
t = Tinggi (cm)
Cara Menggambar Tabung
- Pertama, gambar alas tabung memiliki bentuk ellips atau lonjong yang menunjukkan bahwa alas tersebut merupakan dua buah lingkaran.
- Kemudian, tarik garis tegak lurus serta sama panjang di kedua tepi lingkaran.
- Lalu, gambar tutup tabung kongruen dengan sisi alas.
- Selanjutnya, jadilah gambar tabung.
Kerucut
Kerucut adalah salah satu bangun ruang yang mempunyai sebuah alas yang berbentuk lingkaran dengan selimut yang memiliki irisan dari lingkaran.
Sisi tegak pada kerucut berupa bidang miring yang disebut selimut kerucut. Sisi lainnya disebut alas kerucut. Maka dapat disimpulkan, bahwa kerucut hanya memiliki 2 sisi, dan satu rusuk. Berikut ini gambar kerucut:
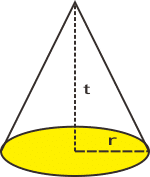
Ciri-Ciri Kerucut
Ciri-ciri kerucut diantaranya yaitu:
- Kerucut merupakan bangun ruang berbentuk limas yang alasnya berbentuk lingkaran.
- Kerucut memiliki 2 sisi.
- Kerucut memiliki 1 rusuk.
- Kerucut memiliki 1 titik puncak.
- Kerucut memiliki jaring-jaring kerucut yaitu lingkaran dan segi tiga.
Sifat-Sifat Kerucut
Berikut ini sifat-sifat kerucut, diantaranya yaitu:
- Kerucut memiliki 2 sisi (1 sisi merupakan alas yang berbentuk lingkaran dan 1 sisinya lagi berupa sisi lengkung atau selimut kerucut)
- Kerucut memiliki 1 rusuk lengkung
- Kerucut tidak memiliki rumus titik sudut.
- Kerucut memiliki 1 buah titik puncak.
Unsur-Unsur Kerucut
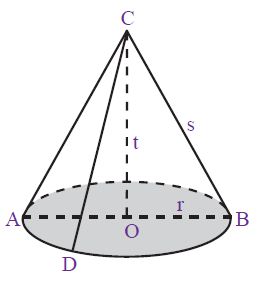
Berikut ini unsur atau bagian kerucut, diantaranya yaitu:
- Bidang alas, yaitu sisi yang berbentuk lingkaran (daerah yang diarsir).
- Diameter bidang alas (d), yaitu ruas garis AB.
- Jari-jari bidang alas (r), yaitu garis OA dan ruas garis OB.
- Tinggi kerucut (t), yaitu jarak dari titik puncak kerucut ke pusat bidang alas (ruas garis CO).
- Selimut kerucut, yaitu sisi kerucut yang tidak diarsir.
- Garis pelukis (s), yaitu garis-garis pada selimut kerucut yang ditarik dari titik puncak C ke titik pada lingkaran.
Hubungan antara r, s, dan t pada kerucut tersebut di atas dapat dinyatakan dengan persamaan-persamaan berikut, yang bersumber dari teorema pythagoras, yaitu:
s² = r² + t²
r² = s² – t²
t² = s² – r²
Rumus Kerucut
Rumus Volume Kerucut
V = 1/3πr².t
Rumus Luas Permukaan Kerucut
L = Luas Lingkaran + Luas Selimut
L = πr²+ trs atau
L = πr. (r+s)
Rumus Luas Alas Kerucut
L = πr²
Rumus Luas Selimut Kerucut
L = πrs
Keterangan:
r = jari-jari (cm)
T = tinggi (cm)
π = 22/7 atau 3,14
Bola
Bola adalah bangun ruang tiga dimensi yang dibentuk oleh titik-titik yang berjarak sama terhadap suatu titik yang disebut titik pusat bola dan bola hanya memiliki 1 sisi.
Dimensi bola dinyatakan dalam besaran jari-jari (r) atau diameter (d). Jari-jari atau radius bola adalah jarak antara permukaan bola dan titik pusat bola, sedangkan diameter bola adalah jarak garis lurus antara permukaan bola dengan permukaan sebrang titik pusat melalui titik pusat bola atau bisa dikatakan bahwa diameter bola sama dengan dua kali jari-jari bola.
Permukaan bola atau disebut juga kulit bola atau selimut bola adalah bidang yang membentuk permukaan bola. Luas permukaan bola atau disebutjuga luas kulit bola atau luas selimut bola. Gambar Bola:
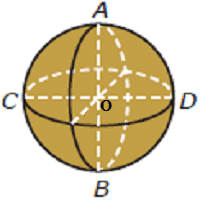
Sifat-Sifat Bola
- Berikut ini sifat atau ciri-ciri bola, diantaranya yaitu:
- Memiliki 1 buah bidang sisi.
- Memiliki 1 buah titik pusat.
- Memiliki 1 sisi lengkung tertutup.
- Tidak memiliki bidang datar.
- Tidak memiliki titik sudut dan rusuk.
- Memiliki jari jari yang tak terhingga dan semuanya sama panjang.
- Ruang garis yang menghubungkan dua titik pada bola disebut tali busur bola dan tali busur bola terpanjang disebut diameter bola.
Unsur-Unsur Bola
Berikut ini unsur-unsur dalam bangun ruang bola, diantaranya yaitu:
Jari-Jari
Jari-jari (r) adalah jarak dari titik pusat ke titik lain diluar bola.
Diameter
Diameter (d) adalah jarak antara dua titik terluar bola yang melewati titik pusat bola. Panjang diameter sama dengan 2x panjang jari-jari.
Sisi
Sisi adalah kumpulan titik yang berjarak sama dengan titik pusat.
Titik Pusat
Titik pusat bola adalah lokasi titik inti pada ukuran bola.
Rumus Bola
Rumus Luas Permukaan Bola
L= 4πr²
Rumus Luas Permukaan 3/4 Bola (Berongga)
Luas permukaan = 3/4 × Luas permukaan bola
Luas permukaan = 3/4 × 4 × π × r²
Luas permukaan = 3πr²
Rumus Luas Permukaan 3/4 Bola Pejal
Luas permukaan = 3/4 × Luas permukaan Bola + Luas alas Lingkaran Bola
Luas permukaan = 3/4 × 4 × π × r² + π × r²
Luas permukaan = 3 × π × r² + π × r²
Luas permukaan = 4πr²
Rumus Luas Permukaan 1/2 Bola (Berongga)
Luas permukaan = 1/2 × LP Bola
Luas permukaan = 1/2 × 4 × π × r²
Luas permukaan= 2πr²
Rumus Luas Permukaan 1/2 Bola Pejal
Luas permukaan = 1/2 × Luas permukaan Bola + Luas alas Lingkaran Bola
Luas permukaan = 1/2 × 4 × π × r² + π × r²
Luas permukaan = 2 × π × r² + π × r²
Luas permukaan = 3πr²
Rumus Luas Permukaan 1/4 Bola (Berongga)
Luas permukaan = 1/4 × Luas permukaan Bola
Luas permukaan = 1/4 × 4 × π × r²
Luas permukaan = πr²
Rumus Luas Permukaan 1/4 Bola Pejal
Luas permukaan = 1/4 × Luas permukaan Bola + Luas alas Lingkaran Bola
Luas permukaan = 1/4 × 4 × π × r² + π × r²
Luas permukaan = π × r² + π × r²
Luas permukaan = 2πr²
Rumus Volume Bola
Volume = 4/3 x π × r³
Rumus Volume Seperempat Bola dan Bola Pejal Tiga Seperempat
V = 3/4 × 4/3 × π × r³
V = πr³
Rumus Volume Setengah Bola dan Bola Pejal Setengah
V = 1/2 × 4/3 × π × r³
V = 2/3 × π × r³
Rumus Volume Seperempat Bola dan Bola Pejal Seperempat
V = 1/4 × 4/3 × π × r³
V = 1/3 × π × r³
Contoh Soal Bangun Ruang Sisi Lengkung
Berikut ini contoh soal bangun ruang sisi lengkung dan pembahasannya:
1. Diketahui pada sebuah tabung mempunyai ukuran jari-jari 10 cm dan tinggi 30 cm. Maka coba hitunglah:
a. volume tabung
b. luas alas tabung
c. luas selimut tabung
d. luas permukaan tabung
Pembahasan:
a. Volume tabung
V = πr²t
V = 3,14 x 10 x 10 x 30 = 9432 cm³
b. Luas alas tabung
L = π r²
L = 3,14 x 10 x 10 = 314 cm²
c. Luas selimut tabung
L = 2 π r t
L = 2 x 3,14 x 10 x 30
L = 1884 cm²
d. Luas permukaan tabung
Luas permukaan tabung = luas selimut + luas alas + luas tutup (luas tutup = luas alas)
L = 1884 + 314 + 314= 2512 cm²
2. Tentukan volume kerucut terpancung jika diameter alasnya 10 dm, diameter sisi atas 4 dm, dan tinggi 4 dm!
Pembahasan:
Diketahui:
diameter alasnya 10 dm, jadi jari-jari alas = 5dm
diameter sisi atas 4 dm, jadi jari-jari atas = 2dm
tinggi = 4 dm
Jawab:
V = π ×t (r.alas² + r.alas × r.atas + r.atas² )
V = 3,14 × 4dm (5dm x 5 dm + 5dm × 2dm + 2dm × 2dm)
V = 12,56 dm (25dm² + 10dm² + 4dm²)
V = 12,56 dm (39dm²)
V = 12,56 dm × 39dm²
V = 489,84dm³
3. Sebuah kerucut memiliki tinggi 8 cm dan jari jarinya 6 cm. Tentukan luas selimut kerucut, luas permukaan kerucut dan volume kerucut!
Pembahasan:
Diketahui:
t = 8 cm
r = 6 cm
Ditanya: luas selimut,luas permukaan dan volume?
Jawab:
Pertama, mencari nilai s (garis lukis):
s² = r² + t²
s² = 6² + 8²
s² = 36 + 64
s² = 100
s = √100 = 10 cm
a. Luas Selimut
L = πrs
L = 3,14 x 6 x 10
L =188,4 cm²
b. Luas Permukaan
L = πr (s + r)
L = 3,14 x 6 (10 + 6)
L = 18,84 x 16
L = 301,44 cm²
c. Volume Kerucut
V = 1/3 πr²t
V = 1/3 x 3.14 x 6² x 8
V = 301,44 cm³
4. Sebuah balon udara berbentuk bola dan terbuat dari bahan elastis. Berapakah luas bahan yang dibutuhkan untuk membuat balon udara tersebut jika diameternya 28 m dengan π=22/7!
Pembahasan:
Diketahui:
d = 28 → r = 14
π= 22/7
Ditanyakan: luas?
Jawab:
L = 4πr²
L = 4×22/7×14×14
L = 2.464 m²
Jadi luas bahan yang dibutuhkan adalah 2.464 m²
5. Sebuah bola besi dimasukan kedalam tabung plastik terbuka di bagian atasnya. Tabung tersebut kemudian diisi dengan air hingga penuh. Jika diameter datinggi tabung sama dengan diameter bola yakni 60 cm, maka hitunglah volume air yang tertampung oleh tabung!
Pembahasan:
Diketahui:
r tabung = 30 cm
rbola = 30 cm
ttabung = 60 cm, sehingga:
Ditanya: volume air dalam tabung?
Jawab:
V tabung = πr²t
V tabung = 3,14 x 30 x 30 x 60
V tabung = 169.560 cm³
V bola = 4/3 π r3
V bola = 4/3 x 3,14 x 30 x 30 x 30
V bola = 113.040 cm³
V air = V tabung − V bola
V air = 169.560 − 113.040 = 56.520 cm³
6. Berapakah volume bola jika diketahui jari-jarinya 5 cm?
Pembahasan:
Diketahui:
r = 5 cm
Ditanya: V?
Jawab: :
V = 4/3 πr³
V = 4/3 x 3,14 x 5³
V = 523,33 cm³
7. Panjang jari-jari alas dari suatu tabung yaitu = 10,5 cm serta tingginya = 20 cm. Untuk π = 22/7 hitunglah:
a. Luas selimut tabung
b. Luas tabung tanpa tutup
c. Luas tabung seluruhnya
Pembahasan:
Diketahui:
r = 10,5 cm
t = 20 cm
π = 22/7
Ditanya:
a. Luas selimut?
b. Luas tabung tanpa tutup?
c. Luas tabung seluruhnya ?
Jawab:
a. Luas selimut tabung
Luas selimut tabung = 2πrt
Luas selimut tabung = 2 × 22/7 × 10,5 × 20
Luas selimut tabung = 1.320 cm²
b. Luas selimut tanpa tutup
Luas selimut tanpa tutup = πr² + 2πrt
Luas selimut tanpa tutup = (22/7×10,5×10,5) + (2×22/7×10,5×20)
Luas selimut tanpa tutup = 346,5 + 1.320
Luas selimut tanpa tutup = 1.666,5 cm²
c. Luas tabung seluruhnya
Luas tabung seluruhnya = 2πr(r+t)
Luas tabung seluruhnya = 2×22/7×10,5×(10,5+20)
Luas tabung seluruhnya = 2.013 cm²
8. Sebuah tabung memiliki jari-jari 10 cm dan tinggi 30 cm. Hitunglah:
a. volume tabung
b. luas alas tabung
c. luas selimut tabung
d. luas permukaan tabung
Pembahasan:
a. Volume tabung
V = πr²t
V = 3,14 x 10 x 10 x 30
V = 9432 cm³
b. Luas alas tabung
L = πr²
L = 3,14 x 10 x 10
L = 314 cm²
c. Luas selimut tabung
L = 2 π r t
L = 2 x 3,14 x 10 x 30
L = 1884 cm²
d. Luas permukaan tabung
Luas permukaan tabung = luas selimut + luas alas + luas tutup (luas tutup = luas alas)
L = 1884 + 314 + 314 = 2512 cm²
9. Perhatikan gambar dibawah ini!
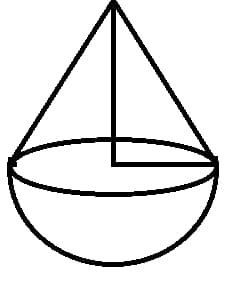
Diketahui, jari-jari = 7 cm dan tinggi = 24 cm , maka tentukan:
a. Volume
b. Jika 1 cm³ beratnya 12 gr maka ,hitunglah berat benda tersebut!
c. Luas permukaan benda tersebut!
Pembahasan:
Diketahui:
r = 7
t = 24
Jawab :
a. Volume benda = V kerucut + V setengah bola
Volume benda = 1/3 πr² t + 2/3 πr3
Volume benda = 1/3 x 22/7 x 7² x 24 + (2/3 x 22/7 x 7³)
Volume benda = 1232 + 718,67
Volume benda = 1950,67 cm³
b. Berat benda = 1950,67 x 12 gr
Berat benda = 23408,04 gr
Berat benda = 23,40804 kg
c. s = √7² + 24²
s = √49 + 576
s = √ 625
s = 25
Lselimut = πrs
Lselimut = 22/7 x 7 x 25
Lselimut = 550 cm²
L setengah bola berongga = 2πr²
L setengah bola berongga = 2 x 22/7 x 7 x 7
L setengah bola berongga= 308 cm²
Lpermukaan benda = Lsel + Lsetbola
Lpermukaan benda = 550 + 308
Lpermukaan benda = 858 cm²
10. Volume sebuah bola 381,51 cm³, berapakah jari-jari bola tersebut!
Pembahasan:
Diketahui:
v bola = 381,51 cm³
Ditanya : jari-jari (r)?
Jawab:
V = 4/3 πr³
381,51 = 4/3 x 3,14 x r³
r³ = (381,51 x 3) : (4 x 3,14)
r³ = 91,125
r = 4,5 cm
Demikian artikel pembahasan tentang pengertian bangun ruang sisi lengkung, jenis, unsur, rumus, contoh soal bangun ruang sisi lengkung dan pembahasannya secara lengkap. Semoga Bermanfaat













0 komentar:
Posting Komentar